이차함수를 유치원생에게 설명
"이차함수는 무엇일까?"
- U자 모양의 그림
이차함수는 마치 미끄럼틀처럼 생긴 U자 모양의 그림이에요. 어떤 미끄럼틀은 위로 올라가고, 어떤 미끄럼틀은 아래로 내려가요. - 숫자와 그림의 연결
숫자를 넣으면 미끄럼틀 위의 점이 어디에 있는지 알 수 있어요. 예를 들어, 숫자 1을 넣으면 미끄럼틀 위의 한 점이 생기고, 숫자 2를 넣으면 또 다른 점이 생겨요. 이렇게 여러 점을 이어서 그리면 멋진 U자가 만들어져요. - 꼭짓점 이야기
이 미끄럼틀에는 꼭대기나 바닥 같은 특별한 점이 있어요. 이 점을 "꼭짓점"이라고 불러요. 꼭짓점은 미끄럼틀에서 가장 높은 곳이나 가장 낮은 곳이에요. - 대칭성
이 미끄럼틀은 양쪽이 똑같이 생겼어요. 그래서 왼쪽과 오른쪽이 대칭이에요. 마치 나비의 날개처럼요!
"어떻게 놀 수 있을까?"
- 우리가 숫자를 넣어서 점을 찍고, 그 점들을 이어서 멋진 U자를 만들어볼 수 있어요.
- 그리고 "꼭짓점은 어디에 있을까?", "미끄럼틀이 위로 가는 걸까, 아래로 가는 걸까?" 같은 질문을 하면서 상상력을 키울 수 있어요.
이렇게 이차함수를 놀이처럼 설명하면 아이들이 쉽게 이해하고 흥미를 가질 수 있습니다!
이차함수를 초등학생에게 설명하려면 쉽고 직관적으로 접근해야 합니다. 다음과 같은 방식으로 설명할 수 있습니다:
"이차함수는 무엇일까?"
- 미끄럼틀처럼 생긴 그림
이차함수는 마치 미끄럼틀처럼 생긴 곡선이에요. 어떤 미끄럼틀은 위로 올라가고, 어떤 미끄럼틀은 아래로 내려가요. 이 곡선을 "포물선"이라고 부르기도 해요13. - 숫자와 그림의 연결
숫자를 넣으면 미끄럼틀 위의 점이 어디에 있는지 알 수 있어요. 예를 들어, 숫자 1을 넣으면 미끄럼틀 위의 한 점이 생기고, 숫자 2를 넣으면 또 다른 점이 생겨요. 이렇게 여러 점을 이어서 그리면 멋진 곡선이 만들어져요23. - 꼭짓점 이야기
이 미끄럼틀에는 꼭대기나 바닥 같은 특별한 점이 있어요. 이 점을 "꼭짓점"이라고 불러요. 꼭짓점은 미끄럼틀에서 가장 높은 곳이나 가장 낮은 곳이에요23.
"어떻게 움직일까?"
- 미끄럼틀을 옮기기
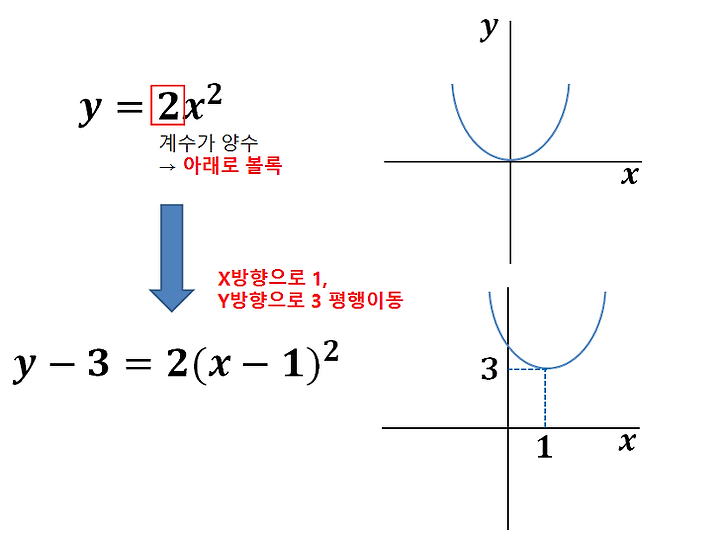
이차함수의 그래프는 움직일 수도 있어요! 미끄럼틀을 왼쪽이나 오른쪽으로 옮기거나, 위로 올리거나 아래로 내릴 수 있어요. 이를 "평행이동"이라고 해요5. - 모양은 그대로 유지
미끄럼틀을 옮겨도 모양은 변하지 않아요. 꼭짓점만 새로운 위치로 이동해요. 예를 들어, 원래 꼭짓점이 (0,0)(0, 0)에 있던 미끄럼틀을 오른쪽으로 3칸 옮기면 꼭짓점이 (3,0)(3, 0)으로 바뀌어요5.
"어떻게 놀 수 있을까?"
- 우리가 숫자를 넣어서 점을 찍고, 그 점들을 이어서 멋진 곡선을 만들어볼 수 있어요.
- 그리고 "꼭짓점은 어디에 있을까?", "미끄럼틀이 위로 가는 걸까, 아래로 가는 걸까?" 같은 질문을 하면서 상상력을 키울 수 있어요.
초등학생에게 이차함수를 설명할 때는 시각적이고 놀이처럼 접근하면 이해하기 쉽고 재미있을 것입니다!
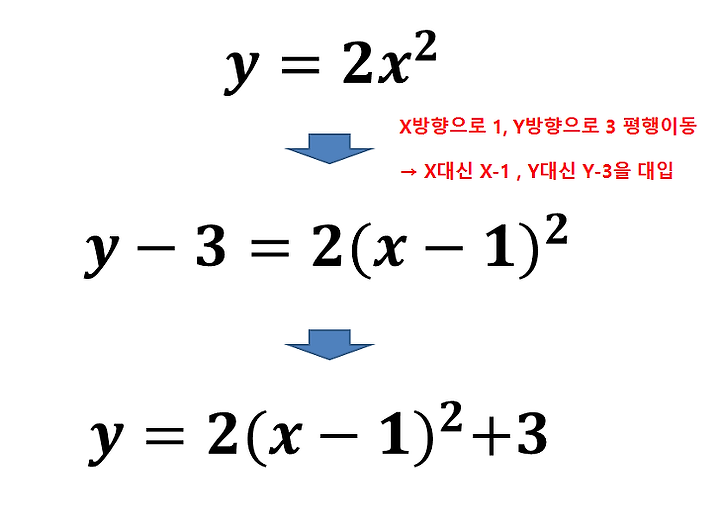


이차함수의 그래프를 쉽게 그리는 방법은 다음과 같은 단계로 설명할 수 있습니다:
1. 이차함수의 형태 확인하기
이차함수는 일반적으로 y=ax2+bx+cy = ax^2 + bx + c 또는 y=a(x−h)2+ky = a(x-h)^2 + k 형태로 주어집니다.
2. 꼭짓점 구하기
- 꼭짓점은 그래프의 가장 높은 점(최대값) 또는 가장 낮은 점(최소값)입니다.
- 일반형 y=ax2+bx+cy = ax^2 + bx + c에서 꼭짓점의 x좌표는 다음 공식으로 계산합니다:x=−b2ax = -\frac{b}{2a}
- 이 값을 원래 식에 대입하여 y좌표를 구하면 꼭짓점의 좌표를 얻을 수 있습니다35.
3. 대칭축 확인하기
- 대칭축은 꼭짓점을 기준으로 좌우 대칭인 축입니다.
- 대칭축은 꼭짓점의 x좌표와 동일하며, 이를 기준으로 그래프를 그립니다6.
4. y절편과 x절편 구하기
- y절편: x=0x = 0일 때의 yy 값으로, 그래프가 y축과 만나는 점입니다.
- x절편: y=0y = 0일 때의 xx 값으로, 그래프가 x축과 만나는 점입니다. 이를 통해 그래프를 더 정확히 그릴 수 있습니다58.
5. 몇 개의 점 계산하여 좌표 찍기
- 여러 개의 xx 값을 선택하고 대응하는 yy 값을 계산하여 점을 찍습니다.
- 예를 들어, y=x2y = x^2라면 다음과 같은 표를 작성할 수 있습니다:
| -2 | 4 |
| -1 | 1 |
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |
이 점들을 좌표평면에 찍고 부드럽게 연결하면 포물선이 완성됩니다36.
6. 그래프 그리기
- 꼭짓점과 절편을 포함하여 찍은 점들을 부드럽게 연결하여 포물선 형태를 만듭니다.
- 그래프가 위로 볼록인지 아래로 볼록인지 확인하면서 방향을 결정합니다45.
7. 연습하기
이 과정을 따르면 이차함수의 그래프를 쉽고 정확하게 그릴 수 있습니다!
유치원생에게 이차함수를 설명하려면 재미있게 그림으로 이야기해 볼게요. 🌈
🎢 놀이공원의 롤러코스터 이야기
- 이차함수는 놀이공원의 롤러코스터 모양을 생각하면 돼!
- 우리가 롤러코스터를 타면 높이 올라갔다가 다시 내려오거나, 내려갔다가 다시 올라가기도 하지? 그 모양이 바로 활처럼 생긴 곡선이야. (🏔모양 또는 🌈모양)
🖍️ 그림으로 표현하기
- 흰 종이에 커다란 무지개 모양을 그려봐! 🎨 (활처럼 휘어진 곡선)
- 롤러코스터가 위로 올라갔다가 내려오는 모습을 생각하면서 그리면 돼!
📖 쉽게 기억하기
- 이차함수는 “무지개 모양” 또는 **“롤러코스터 모양”**을 만들어주는 규칙이야.
- 우리 눈에 보이는 건 곡선이지만, 사실은 숫자들이 규칙대로 모여서 만들어진 거야! 🤹♂️
✨ 재미있는 사실!
- 우리가 공을 위로 던지면 높이 올라갔다가 다시 떨어지지? 이때도 이차함수가 그 모양을 만들어줘! 🏀⬆️⬇️
이차함수는 사실 우리 주변에 많이 숨어 있어요! 🤩 유치원생도 그림으로 이해할 수 있도록 재미있게 설명해봤어요.

유치원생도 쉽게 이해할 수 있도록 이차함수의 그래프를 주인공으로 한 동화책 내용. 제목은 **《무지개 곡선 나라의 모험》**. 🌈📖
🌈 《무지개 곡선 나라의 모험》
옛날 옛날, 숫자 마을에 사는 꼬마 아이 포포는 그림 그리기를 아주 좋아했어요. 특히, 무지개처럼 활 모양으로 휘어진 선을 그리는 걸 제일 좋아했죠. 🎨
어느 날, 포포는 신기한 책을 발견했어요. 책 속에는 이렇게 쓰여 있었어요.
“무지개 곡선 나라로 가려면 활 모양의 다리를 건너야 해!”
포포는 설레는 마음으로 책 속 세상으로 들어갔어요. 그리고 무지개 곡선 다리를 만났죠! 🌉

그 다리는 그냥 똑바른 다리가 아니라, 부드럽게 휘어진 무지개 모양이었어요.
“우와! 이게 바로 이차함수의 그래프라는 거야!”
포포는 다리를 건너면서 다리의 모양을 눈으로 따라 그려봤어요.
“높이 올라갔다가 다시 내려오는 이 모양... 완전히 무지개잖아!” 🌈
다리 너머에는 곡선 동물 친구들이 살고 있었어요. 🦄🐢🦋
- 🦄 활 모양 유니콘: "나는 이차함수 나라의 지킴이야! 우리나라는 항상 이 멋진 모양으로 이어져 있어."

- 🐢 둥글게 걷는 거북이: "나는 천천히 다리를 건너면서 곡선 길을 느끼는 게 좋아!"
- 🦋 날개를 활짝 펴는 나비: "이 곡선 모양 덕분에 내가 하늘 높이 날 수 있어!"
포포는 친구들과 함께 놀면서 이차함수의 그래프를 이해하게 되었어요.
“활 모양이 위로 올라갔다가 내려오는 것도 있고, 반대로 내려갔다가 올라오는 것도 있네!”
마침내 포포는 무지개 곡선 나라에서 즐거운 하루를 보내고 다시 집으로 돌아왔어요.
이제 포포는 어떤 그림을 그려도 자신 있게 무지개 곡선을 그릴 수 있게 되었답니다. 🌈😊
😊

